4. La Segunda Ley de la Termodinamica y sus Aplicaciones.
Contenido:
4. Introduccion.
4.1. Máquinas térmicas y refrigeradores.
4.2. Enunciados de la Segunda Ley.
4.3. Procesos reversibles e irreversibles.
4.4. Ciclo de Carnot.
4.5. Entropía.
4.6. Exergía.
4.7. Trabajo reversible.
4.8. Balance de exergía en sistemas
abiertos.
4.9. Balance de exergía en sistemas cerrados.
----- Referencias y Bibliografía
4. Introducción.
La
energía es una propiedad conservada y no se sabe de ningún proceso que viole la
primera ley de la termodinámica. Por lo tanto es razonable concluir que para
que ocurra, un proceso debe satisfacer la primera ley. Sin embargo,
satisfacerla no asegura que en realidad el proceso tenga lugar. Un proceso no
puede ocurrir a menos que satisfaga tanto la primera ley de la termodinámica
como la segunda. Sin embargo, el uso de la segunda ley de la termodinámica no
se limita a identificar la dirección de los procesos, también afirma que la
energía tiene calidad así como cantidad. La primera ley se relaciona con la cantidad
de energía y sus transformaciones sin considerar su calidad. Conservar la calidad
de la energía es una cuestión importante, y la segunda ley provee los medios
necesarios para determinarla, así como el grado de degradación que sufre durante
un proceso; se usa también para determinar los limites teóricos en el desempeño
de sistemas de ingeniería de uso ordinario, así como predecir el grado de
terminación de las reacciones químicas.
4.1. Máquinas térmicas y refrigeradores.
Una máquina térmica es un dispositivo que convierte energía térmica en otras formas
útiles de energía, como la energía eléctrica y mecánica. Hace que una sustancia
de trabajo recorra un proceso cíclico durante el cual:
1) Se absorbe calor de una fuente a alta
temperatura.
2) La máquina realiza un trabajo
3) Libera calor a una fuente a temperatura
más baja.
En un proceso característico para producir
electricidad en una planta de potencia, el carbón o algún otro tipo de combustible
se quema y el calor generado se utiliza para producir vapor de agua. El vapor
se quema y el calor generado se utiliza para producir vapor de agua. El vapor
se dirige hacia las aspas de una turbina, poniéndola a girar. Por último, la
energía mecánica asociada a dicha rotación se usa para mover un generador
eléctrico. El motor de combustión interna en un automóvil extrae calor del
combustible en combustión y convierte una fracción de esta energía mecánica.
Una máquina térmica transporta alguna sustancia
de trabajo a través de un proceso cíclico, definido como aquel en el que la
sustancia regresa a su estado inicial.
El trabajo neto W realizado por la máquina
es igual al calor neto que fluye hacia la misma.
Se observa que Qneto= Qh-Qc ; por lo tanto:
W=Qh-Qc
Donde Qh y Qc se toman como cantidades
positivas. Si la sustancia de trabajo es un gas, el trabajo neto realizado en
un proceso cíclico es el área encerrada por la curva que representa a tal
proceso en un diagrama PV.
La eficiencia térmica , e, de una máquina
térmica se define como la razón del trabajo neto realizado al calor absorbido
durante un ciclo:
e=W = Qh-Qc=1-Qc
Un frigorífico o un aparato de aire
acondicionado son ejemplos de refrigeradores. En su uso habitual, lo que
hacen los refrigeradores y aparatos de aire acondicionado es principalmente,
mantener constante la temperatura del interior de una cámara o habitación,
expulsado de forma continua el calor que va entrando por las paredes (aparte,
si se introduce un objeto caliente en un frigorífico, éste se encarga de bajar
la temperatura del objeto, consumiendo un trabajo adicional).
Proceso:
1) Extrae calor de un foco frío.
2)El calor se extrae del foco
frío realizando trabajo y se frío realizando trabajo y secede al foco caliente.
3)La sustancia de refrigeración
puede ser agua, aire, gasoilina.
A diferencia del rendimiento de una máquina
térmica, el coeficiente de desempeño puede ser mayor que la unidad (normalmente
lo es, de hecho).
Dado que refrigeradores y bombas de calor operan
en ciclos, el coeficiente de desempeño puede definirse en términos de los
flujos de calor y trabajo.4.2. Enunciados de la Segunda Ley.
Enunciado de Kelvin-Planck, es imposible que un sistema realice un proceso
cíclico cuyos únicos efectos sean el flujo de calor desde una fuente de calor
al sistema y la realización, por parte del sistema, de una cantidad equivalente
de trabajo.
La segunda ley impide la existencia de una
máquina capaz de convertir todo el calor que absorbe en trabajo durante un
proceso cíclico.
Se entiende por fuente de calor (o foco de
calor) un cuerpo suficientemente grande para que el flujo de calor entre él y
el sistema no provoque cambio de temperatura en el foco (el océano, es un buen
foco de calor).
Enunciado de Clausius, es imposible que un sistema realice un proceso
cíclico cuyos únicos efectos sean el flujo de calor hacia el sistema desde una
fuente fría y el flujo de una cantidad igual de calor desde el sistema hacia la
fuente caliente.
El sistema de Clausius es una máquina frigorífica y para funcionar necesita que se realice trabajo sobre el sistema.
4.3. Procesos reversibles e irreversibles.
Reversibles
Un proceso reversible se define como un
proceso que se puede invertir sin dejar ningún rastro en los alrededores.
Es decir, tanto el sistema como los
alrededores vuelven a sus estados iniciales una vez finalizado el proceso
inverso. Esto es posible solo si el intercambio de calor y trabajo neto entre
el sistema y los alrededores es cero para el proceso combinado (original e
inverso). Los procesos que no son invertibles se denominan procesos
irreversibles.
Es posible volver un sistema a su estado
original siguiendo un proceso, sin importar si este es reversible o
irreversible. Pero para procesos reversibles, esta restauración se hace sin
dejar ningún cambio neto en sus alrededores normalmente hacen algún trabajo
sobre el sistema, por lo tanto no vuelven a su estado original.
Los Procesos reversibles en realidad no
ocurren en la naturaleza, solo son idealizaciones de procesos reales. Los
reversibles se pueden aproximar mediante dispositivos reales, nunca se pueden
lograr; es decir, todos los procesos que ocurren en la naturaleza son
irreversibles.
Quizá nunca se tenga un proceso reversible,
pero es posible aproximarse. A medida que se tiene hacia un proceso reversible,
un dispositivo entrega el mayor trabajo posible y consume el menor trabajo.
Irreversibilidades
Los factores que causan que un proceso sea
irreversible se llaman irreversibilidades, las cuales son:
· La fricción: Es una forma familiar de
irreversibilidad relacionada con cuerpos en movimiento. Cuando dos cuerpos en
contacto son forzados a moverse uno respecto al otro. Mientras más grandes sean
las fuerzas de fricción, más irreversible es el proceso. La fricción no siempre
tiene relación con dos cuerpos sólidos en contacto.
· La expansión libre
· El mezclado de dos fluidos
· La transferencia de calor a través de una
diferencia de temperatura finita: La transferencia de calor puede ocurrir solo
cuando hay una diferencia de temperatura entre un sistema y sus alrededores,
por lo tanto es físicamente imposible tener un proceso de transferencia de
calor se vuelve cada vez menos reversible a medida que la diferencia de
temperatura entre los dos cuerpos se aproxima a cero.
· La resistencia eléctrica
· La deformación inelástica de solidos
· Las reacciones químicas4.4. Ciclo de Carnot.
Es un ciclo reversible que consta de dos
etapas isotérmicas a diferente temperatura y dos etapas adiabáticas. La sustancia de trabajo puede no ser un gas
ideal, pero en este desarrollo por simplicidad usaremos un mol de gas ideal.
La
primera etapa del ciclo es una expansión reversible isotérmica (línea 1-2). En
este paso se absorbe una cantidad de calor del foco caliente. La segunda etapa
es una expansión adiabática desde la temperatura del foco caliente a la
temperatura del foco frío (línea 2-3).
La tercera etapa es una compresión isotérmica que cede una cantidad de
calor al foco frío (línea 3-4). La última etapa es la compresión adiabática
que lleva al sistema al punto de partida (línea 4-1).
4.5. Entropía.
La segunda
ley de la termodinámica conduce frecuentemente a expresiones que involucran
desigualdades. Por ejemplo, una máquina térmica irreversible (es decir, real)
es menos eficaz que otra reversible que opera entre los mismos dos depósitos de
energía térmica. Igualmente, un refrigerador irreversible o una bomba de calor
tiene un coeficiente de desempeño (COP) menor que otro reversible que funciona
entre los mismos límites de temperatura. Este concepto se expresa como
Es decir, la integral
cíclica de SQ/T siempre es menor o igual a cero. Esta desigualdad es válida
durante todos los ciclos, tanto reversibles como irreversibles. El símbolo ∫  (símbolo de integral con
un círculo en medio) se usa para indicar que la integración será realizada durante
el ciclo entero. Cualquier transferencia de calor hacia o desde un sistema
consiste en cantidades diferenciales de transferencia de calor. Entonces la
integral cíclica de SQ/T puede considerarse como la suma de todas estas
cantidades diferenciales de transferencia de calor dividida entre la
temperatura en la frontera.
(símbolo de integral con
un círculo en medio) se usa para indicar que la integración será realizada durante
el ciclo entero. Cualquier transferencia de calor hacia o desde un sistema
consiste en cantidades diferenciales de transferencia de calor. Entonces la
integral cíclica de SQ/T puede considerarse como la suma de todas estas
cantidades diferenciales de transferencia de calor dividida entre la
temperatura en la frontera.
Para
demostrar la validez de la desigualdad de Clausius, considere un sistema conectado
a un depósito de energía térmica con una temperatura termodinámica constante
(es decir, absoluta) TR a través de
un dispositivo cíclico reversible (Fig. 1). El dispositivo cíclico recibe calor
del depósito y suministra calor SQ
al
sistema cuya temperatura en esa parte de la frontera es T (una variable) mientras produce trabajo dWrev
El
sistema produce trabajo dWsis como
resultado de esta transferencia de calor. Si se aplica el balance de energía al
sistema combinado identificado por las líneas punteadas, se obtiene
donde SWC es el trabajo total del sistema combinado
(SWrev + SWsis) y dEC es el cambio en la energía total del
sistema combinado. Considerando que el dispositivo cíclico es reversible,
tenemos
donde el
signo de SQ
es
determinado respecto al sistema (positivo si es hacia el sistema y negativo si
es desde el sistema), y el signo de SQR
es
determinado respecto al dispositivo cíclico reversible. Al eliminar SQR de las dos relaciones anteriores
se obtiene
Ahora, si el
sistema experimenta un ciclo mientras el dispositivo cíclico experimenta un
número entero de ciclos, entonces la relación precedente se vuelve
puesto que la integral
cíclica de energía (el cambio neto durante un ciclo en la energía la cual es
una propiedad) es cero. Aquí WC es la integral cíclica
de
SWC, y representa el trabajo neto durante el
ciclo combinado.
Al parecer,
el sistema combinado intercambia calor solamente con un depósito de energía
térmica mientras involucra (produciendo o consumiendo) trabajo WC durante un ciclo. Con
base en el enunciado de Kelvin-Planck de la segunda ley, la cual establece que ningún sistema puede producir una cantidad
neta de trabajo mientras opera en un ciclo e intercambia calor con un solo
depósito de energía térmica, se concluye que WC
no
puede ser un trabajo de salida y por lo tanto no puede ser una cantidad
positiva. Considerando que TR
durante un ciclo. Con
base en el enunciado de Kelvin-Planck de la segunda ley, la cual establece que ningún sistema puede producir una cantidad
neta de trabajo mientras opera en un ciclo e intercambia calor con un solo
depósito de energía térmica, se concluye que WC
no
puede ser un trabajo de salida y por lo tanto no puede ser una cantidad
positiva. Considerando que TR
 es la temperatura
termodinámica y en consecuencia una cantidad positiva, se tiene
es la temperatura
termodinámica y en consecuencia una cantidad positiva, se tiene
que es la
desigualdad de Clausius, la cual es válida para todos los ciclos
termodinámicos, reversibles, irreversibles e incluso los de refrigeración.
Si ninguna
irreversibilidad ocurre tanto dentro del sistema como en el dispositivo cíclico
reversible, entonces el ciclo experimentado por el sistema combinado es
internamente reversible y como tal, puede invertirse. Para un ciclo inverso,
todas las cantidades tienen la misma magnitud pero signo opuesto, por
consiguiente, el trabajo WC, que no
podría ser una cantidad positiva en el caso ordinario, no puede ser una
cantidad negativa en el caso inverso. Entonces, WC,int
rev = 0 puesto que no puede ser una cantidad
positiva o negativa, así
para ciclos
internamente reversibles. De ahí se concluye que la igualdad en la desigualdad de
Clausius se cumple para ciclos reversibles total o sólo internamente reversibles,
mientras que la desigualdad se mantiene para los irreversibles.
Con la finalidad de
desarrollar una relación para la definición de entropía, examinemos más
profundamente la ecuación 2, en la cual se tiene una cantidad cuya integral
cíclica es cero. Pensemos por un momento qué tipo de cantidades pueden tener
esta característica; se sabe que la integral cíclica de trabajo no es cero. (Es
bueno que así sea, ya que de otro modo, las máquinas térmicas que trabajan en
un ciclo, como las centrales termoeléctricas, producirían trabajo neto igual a
cero.) Tampoco lo es la integral cíclica de calor.
Considere el
volumen ocupado por un gas en un dispositivo de cilindro-émbolo que experimenta
un ciclo, como se muestra en la figura 2. Cuando el émbolo vuelve a su posición
inicial al final del ciclo, el volumen del gas también vuelve a su valor
inicial, de manera que el cambio neto en el volumen durante un ciclo es cero,
lo cual se expresa como:

Es decir, la
integral cíclica de volumen (o de cualquier otra propiedad) es cero. Asimismo,
una cantidad cuya integral cíclica es cero depende sólo del estado y no de la
trayectoria del proceso, por lo tanto es una propiedad. En consecuencia, la
cantidad (SQ/T)int,rev debe representar
una propiedad en la forma diferencial. Clausius comprendió en 1865 que él había
descubierto una nueva propiedad termodinámica y decidió nombrarla entropía, la cual está designada por S y definida como:
La entropía
es una propiedad extensiva de un sistema y a veces es llamada entropía total,
mientras que la entropía por unidad de masa s es una propiedad intensiva y tiene
la unidad kJ/kg · K. Generalmente, el término entropía es usado para referirse
a ambas: a la total y a la de por unidad de masa, ya que el contexto normalmente
esclarece de cuál se trata. El cambio de entropía de un sistema durante un
proceso puede determinarse integrando la ecuación 7-4 entre los estados
iniciales y final:
4.6. Exergía.
La Exergía
es una propiedad termodinámica que permite determinar el potencial de trabajo
útil de una determinada cantidad de energía que se puede alcanzar por la
interacción espontánea entre un sistema y su entorno. Informa de la utilidad
potencial del sistema como fuente de trabajo. Es una propiedad termodinámica,
por lo que es una magnitud cuya variación solo depende de los estados inicial y
final del proceso y no de los detalles del mismo.
Dado un sistema combinado formado por un
sistema cerrado y el ambiente (con un volumen total constante y una frontera
que solo permite interacciones de trabajo), la exergía (denotada como A) se
define como el máximo trabajo teórico que puede realizar el sistema combinado
cuando el sistema cerrado evoluciona hasta alcanzar el equilibrio con el
ambiente (i.e. hasta su estado muerto).
Definida de otra forma la exergía es la
porción de la energía que puede ser transformada en trabajo mecánico.
La exergía determina de forma cuantitativa el
valor termodinámico de cualquier recurso, y permite analizar rigurosamente el
desperdicio de los recursos en las actividades de la sociedad, estableciendo
pautas para su ahorro y uso eficiente.4.7. Trabajo reversible.
El
trabajo reversible se define como la cantidad
máxima de trabajo útil que puede obtenerse cuando un sistema experimenta un
proceso entre los estados inicial y final. Ésta es la salida (o entrada) de
trabajo útil que se obtiene cuando el proceso entre los estados inicial y final
se ejecuta de manera reversible.
4.8. Balance de exergía en sistemas abiertos.
La mayoría
de los volúmenes de control encontrados en la práctica, como turbinas, compresores,
toberas, difusores, intercambiadores de calor, tuberías y ductos operan en
forma estacionaria, por lo tanto no experimentan cambio en sus contenidos de
masa, energía, entropía y exergía, así como en sus volúmenes.
Por
consiguiente, dVVC/dt =0 y dXVC/dt = 0 para tales sistemas, y la
cantidad de exergía que entra en un sistema de flujo estacionario en todas las
formas (calor, trabajo, transferencia de masa) debe ser igual a la cantidad de
exergía que sale más la exergía destruida. Entonces la forma de tasa del balance
general de exergía para un proceso de flujo estacionario se reduce a:
Para un dispositivo de flujo estacionario y una sola corriente (una
entrada, una salida), la relación anterior se reduce aún más a:
donde los subíndices 1 y 2 representan los estados de entrada y salida es el flujo másico, y el cambio en la exergía de
flujo está dado por la ecuación como:
。
Entre m se obtiene el balance de exergia por unidad de
masa
ó 。。 。 。
Donde q = Q/m y w = W/m son la transferencia de calor y el trabajo
realizado por unidad de masa del fluido de trabajo, respectivamente.
4.9. Balance de exergía en sistemas cerrados.
La naturaleza de la exergía es opuesta a la de
la entropía, en la cual la exergía puede destruirse
pero no puede crearse. Por consiguiente, el cambio de exergía de un sistema durante un proceso es menor que
la transferencia de exergía por
una cantidad igual a exergía destruida
dentro de las fronteras del sistema durante el proceso. Entonces el principio de disminución de exergía puede
expresarse como:
(cambio en la exergia total del sistema)
ó
Xent
– Xsal – Xdestruida = ΔXsistema
Esta relación se conoce
como el balance de exergía y
puede definirse como:
El cambio de exergía de un sistema durante un proceso es igual a la
diferencia
entre la transferencia neta de exergía
a través de la frontera del sistema y la exergía destruida dentro de las fronteras del sistema como resultado
de las irreversibilidades.
Anteriormente se
mencionó que la exergía puede transferirse hacia o desde un sistema por
transferencia de calor, trabajo y masa. Entonces el balance de exergía para cualquier
sistema que experimenta cualquier proceso puede expresarse más explícitamente
como:
o en forma de tasa como:
donde las tasas de transferencia de exergía por calor, trabajo y masa se
expresan como
El balance de exergía también puede expresarse por unidad de masa como:
Asimismo, normalmente es más conveniente encontrar primero la generación
de entropía Sgen y despues evaluar
Cuando las condiciones ambientales Po
y To así como los estados inicial y final del sistema están especificados, el
cambio de exergía del sistema de
puede ser determinado directamente
de la ecuación sin tomar en cuenta cómo se ejecuta el proceso. Sin embargo,
determinar la transferencia de exergía por calor, trabajo y masa requiere un
conocimiento acerca de estas interacciones.
Un sistema cerrado no involucra flujo
másico, por lo tanto tampoco cualquier transferencia de exergía asociada con el
flujo másico. Si se toma la dirección positiva de la transferencia de calor
hacia el sistema y la dirección positiva de transferencia de trabajo desde el
sistema, el balance de exergía para un sistema cerrado puede expresarse más
explícitamente como:
ó
Referencias y Bibliografía:
- Cengel, Termodinmica, 7a Edicion.












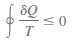













Comentarios
Publicar un comentario